Eh bien, la première étape est d'arrêter de penser que les électrons sont de très petites boules qui gravitent autour du noyau selon un chemin circulaire. Ceci est connu sous le nom de modèle Bohr. Bien que ce modèle soit un excellent modèle au niveau d’introduction, il ne raconte pas toute l’histoire.

Il y a plusieurs problèmes avec la notion que les électrons voyagent sur une orbite circulaire autour du noyau, le principal étant qu'ils devraient éventuellement subir une désintégration orbitale et donc finalement ralentir et s'écraser dans le noyau. Bien sûr, cela n'arrive pas. Alors, comment les électrons se déplacent-ils autour du noyau?

C'est là que la théorie quantique est venue à la rescousse au début du 20e siècle. Il a déclaré que les électrons ne pouvaient pas être traités comme une particule classique et n'avaient pas de position et d'élan définis. Donc, cela signifie essentiellement que nous ne pouvons pas connaître exactement la position d'un électron et son élan en même temps. Cette relation est donnée par le principe d'incertitude de Heisenberg .

Je n'entrerai pas dans les détails car pour garder cette explication basique, mais si vous êtes intéressé, regardez cette vidéo qui fournit une très bonne explication.

Donc, fondamentalement, ce que la théorie quantique nous dit que nous ne pouvons en fait pas spécifier où et quel chemin un électron va prendre. Cependant, le modèle de Bohr suppose que vous pouvez tracer avec précision où un électron va être, mais nous savons maintenant qu'en raison du principe d'incertitude de Heisenberg , vous ne pouvez pas connaître précisément la position exacte et l'élan d'un électron. Nous ne pouvons donc en fait pas construire une orbite et dire que l'électron suivra toujours ce chemin.

Par conséquent, il est impossible de tracer une orbite pour un électron, comment pouvez-vous? Si vous ne savez pas où sera le prochain électron, vous ne pouvez pas prédire son chemin.

Alors, comment pouvons-nous contourner ce problème? Eh bien, si nous ne pouvons pas tracer l’orbite d’un électron, la meilleure chose à faire est de tracer une orbitale de probabilité de densité d’électrons pour celui-ci. Également appelé orbitales atomiques .

Une orbitale est une région bien définie de l'espace. Par conséquent, une orbitale atomique est une région de l'espace qui montre où l'électron sera 95% du temps (généralement nous prenons 95% mais cela pourrait être n'importe quel nombre tel que 90% ou 75%).

Une façon simple de penser aux orbitales est d'imaginer que vous avez une caméra magique capable de prendre une séquence de photos d'un électron dans un atome d'hydrogène. L'électron apparaît comme un point. Maintenant, si nous superposons toutes ces images, vous verrez quelque chose comme ceci:

Puisque nous considérons généralement les orbitales atomiques comme la région de l'espace qui montre où l'électron sera 95% du temps, la sphère très extérieure de l'image ci-dessus est considérée comme l'orbitale de l'électron.

J'espère que cela vous aidera à comprendre les orbitales. Si vous avez des questions, n'hésitez pas à demander.

Pourquoi n'essayez-vous pas les analogies: au moins, en guise d'introduction de base, j'apprécie beaucoup la tentative faite ici par Goh et al.

Une orbitale est définie comme une région de l'espace dans laquelle il existe une forte probabilité de trouver un électron. Une analogie pour une orbitale est la localisation possible d'un élève en fonction de son emploi du temps. Par exemple, selon l'horaire, le lundi à 9h00, un étudiant doit être dans la salle de cours 1 pour un cours de chimie. On peut dire que, sur une période de plusieurs semaines, il y a une forte probabilité que cet étudiant soit dans la salle de cours 1 à ce moment-là ce jour-là. Cependant, on ne peut pas être sûr à 100% que cet élève sera là car il ou elle pourrait s'absenter de l'école ce jour-là. On ne peut généralement pas non plus prédire exactement où l'étudiant s'assiéra dans la salle de conférence, mais on peut dire, avec une forte probabilité, que cet étudiant sera dans l'enceinte de la salle de conférence. Cette analogie décrit assez bien une orbitale, car elle prend en compte la probabilité et la région de l'espace dans la définition d'une orbitale.

Je vais certainement commencer par une analogie qui semble donner une description assez simple, bien que approfondie, de la façon dont les orbitales devraient être considérées.

D'accord. Oubliez tout sur les orbitales pendant une seconde.

Vous avez des noyaux. Vous avez des électrons autour d'eux.

Première étape: les électrons ne sont pas des boules. Imaginez-les comme étant une charge maculée dans l'espace. C'est précisément ce qu'ils sont: une charge maculée dans l'espace, avec des bordures floues, comme une goutte non focalisée. La forme de cette goutte dépend de nombreux facteurs, mais le plus important est la position des noyaux.

Supposons maintenant que vous vouliez décrire la forme de cette goutte, comme si vous vouliez l'imprimer en 3D. Eh bien, un moyen simple serait de diviser l'espace en petits cubes et de dire «charge» si vous avez un frottis ou «sans frais» si vous n'avez pas ce frottis. En pratique, comme c'est flou, on dirait "3.0 charge" dans certains cubes, "1.3 charge" dans d'autres cubes, "0.1 charge" dans d'autres cubes et ainsi de suite. C'est une manière parfaitement légitime de décrire ce que l'on appelle la "densité de charge" dans l'espace.

Le problème avec cette approche est qu'elle est plutôt gênante. Il a une précision médiocre et il évolue mal. Si vous réduisez les petits cubes, parce que vous n'aimez pas vivre dans un monde minecraft, vous avez besoin de beaucoup plus de cubes pour le faire.

Il existe donc maintenant une méthode plus intelligente pour le faire et pour expliquer il, j'ai besoin que vous compreniez la décomposition de Fourier. Ce n'est pas aussi difficile que vous le pensez.

Le problème est le suivant. Vous avez une onde sonore complexe, comme celle produite en sifflant ou en chantant une chanson, et il s'avère que vous pouvez créer n'importe quelle forme complexe de cette onde en sommant des ondes plus simples: un choix judicieux des sinus et cosinus de certaines fréquences (pitch), et avec certaines intensités (volumes). Jouez-les tous ensemble, vous récupérez l'onde initiale.

C'est exactement ce que vous voyez dans votre affichage du spectre dans votre chaîne stéréo

Où chaque colonne est une fréquence différente, et la hauteur de la colonne est l'intensité de cette fréquence particulière. Cela change tout le temps parce que vous jouez de la musique complexe, mais essayez de jouer un son uniforme (par exemple un violon jouant une seule note) et vous verrez qu'il reste le même partout.

Revenons maintenant aux orbitales .

Les orbitales sont les "sinus et cosinus" de notre problème de description de cette goutte. Nous avons une entité complexe (notre tache maculée) et nous voulons la décrire en additionnant «quelque chose». Peu importe le "quelque chose" que nous utilisons, mais il s'avère que les fonctions tridimensionnelles de cette forme ont beaucoup de propriétés intéressantes qui rendent le problème beaucoup plus compact.

Faisons un exemple simple. Supposons que vous ayez une goutte sphérique de charge. C'est probablement bien décrit par une seule orbitale de forme sphérique (une orbitale s), exactement comme une onde sinusoïdale d'un diapason est bien décrite par une seule fonction sinusoïdale.

Maintenant, ajoutez un champ électrique pour que le les électrons sont tirés, et la sphère enduite ressemble maintenant plus à un œuf allongé. Celui-là n'est pas vraiment bien décrit par une sphère, n'est-ce pas? vous devez donc décrire le lobe, ce qui signifie que vous avez besoin d'une orbitale supplémentaire (orbitale ap) à ajouter au mélange afin que le résultat soit en forme d'oeuf, exactement comme vous avez besoin de plus d'une onde sinusoïdale pour décrire le son d'un violon.

C'est tout, vraiment. les orbitales ne sont que des équivalents 3D pratiques du sinus et du cosinus. Nous pourrions bien utiliser n'importe quoi d'autre (et en fait nous le faisons, dans certains cas) et cela fonctionnerait également, mais avec quelques inconvénients potentiels.

Elucider la structure orbitale atomique d'un atome est une histoire fascinante. Il vient d'être résolu au cours des cent dernières années. Ce n'était pas un voyage linéaire, mais un voyage rempli de toutes sortes d'impasses et de voyages secondaires. Les Grecs pensaient que les éléments étaient l'air, le feu, l'eau et la terre. Ne comprenant pas les atomes, les alchimistes ont passé des milliards d'heures et une quantité incalculable d'argent à essayer de transformer d'autres substances en or.

Ainsi, la première étape significative dans la résolution de la structure atomique commence avec Dmitri Mendeleev qui est crédité de la notion de tableau périodique. Cela a permis de découvrir des éléments supplémentaires qui étaient nécessaires pour compléter le tableau. Cependant, la raison pour laquelle la disposition de la table fonctionnait était inconnue.

À peu près à la même époque, d'autres travaux se déroulaient. Maxwell a créé ses célèbres équations liant le courant électrique et le magnétisme.

La découverte de l'électron s'est produite à peu près au même moment. Mais ce n'est que vers 1900 que la compréhension d'un électron fut assez complète.

Les physiciens ne comprenaient toujours pas comment assembler un atome. À ce stade, de nombreux modèles atomiques ont été lancés pour expliquer divers phénomènes. Un de ces modèles était le modèle de pudding à plomb. L'idée était qu'un atome était comme une goutte de pudding dans laquelle les électrons étaient suspendus comme des prunes dans le pudding.

Une grande avancée est venue de la diffusion de Rutherford vers 1910. Ces expériences ont montré que le noyau (charge positive) était situé au centre d'un atome et qu'il avait un très petit volume par rapport à l'atome entier. Cela a conduit au modèle planétaire de l'atome. Les électrons chargés négativement ont tourné autour du noyau chargé positivement comme les planètes en orbite autour du soleil.

Cela n'expliquait pas d'autres phénomènes connus comme les spectres de raies d'hydrogène que Balmer avait découverts avant 1900.

De tels spectres de raies étaient liés via la formule de Rydberg qui liait le nombre quantique principal $ n $ à la structure atomique.

$ \ frac {1} {\ lambda} = R (\ frac {1} {{n_1} ^ 2} - \ frac {1} {{n_2} ^ 2}) $

en 1913, le modèle Bohr a été développé. Cela expliquait que les électrons étaient disposés en coquilles et que le remplissage de la structure de la coquille pouvait être lié au tableau périodique!

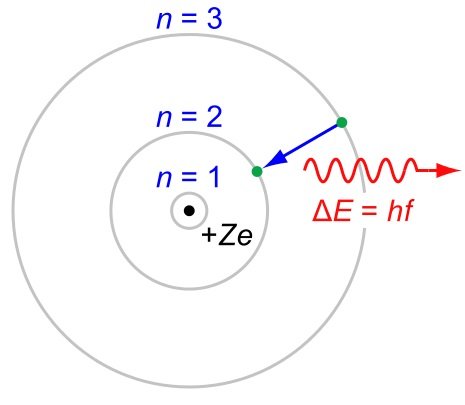
La structure de la coque est fondamentalement fixée sur le modèle planétaire par Arnold Sommerfeld et l'idée était que pour une raison quelconque, les électrons ne pouvaient pas tournent autour du noyau de l'atome dans "n'importe quelle" orbite mais qu'ils devaient occuper certaines orbites qui devinrent connues sous le nom de coquilles. Des sous-couches ($ l $, $ m $ et $ s $) ont été ajoutées au modèle de Bohr pour truquer des orbites supplémentaires afin d'expliquer la structure spectroscopique fine de certains éléments. Comme les raies de Fraunhofer observées dans les spectres du soleil.

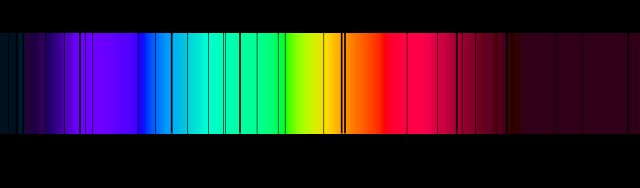
Donc, à ce stade, les physiciens et les chimistes avaient catalogué une grande partie du comportement des atomes, mais n'avaient toujours pas une compréhension complète de la façon dont les atomes travaillé.

Au milieu des années 1920, Schrödinger a développé sa célèbre équation qui a complété le puzzle de la structure des atomes en électrons et noyaux plus fondamentaux. À partir du modèle de Bohr, il a été réalisé que les électrons doivent être sur certaines orbites car les orbites sont quantifiées. C'est-à-dire que chaque orbitale a une énergie spécifique. Ce que Schrödinger a montré, c'est que les orbites n'étaient pas comme les voies d'un événement d'athlétisme qui contraignait les électrons, mais que l'orbite des électrons était distribuée dans un nuage 3D autour de l'atome. Un autre aspect du travail de Schrödinger et d'autres était que l'électron avait à la fois des caractéristiques d'onde et des caractéristiques de particule.

En utilisant l'équation d'onde de Schrödinger, la forme des orbitales peut être calculée. Maintenant, c'était dans les années 1930, les ordinateurs étaient encore à des décennies. Donc ces calculs ont été faits à la main! Le "problème" était que la résolution des équations n'était possible que pour un électron. En utilisant le calcul, il est agréable de pouvoir résoudre des équations afin que les intégrales puissent être facilement calculées. Cependant, le problème des trois corps ne permet pas une telle solution. Avec les ordinateurs modernes, il est possible de calculer des solutions numériques même si les intégrales n'existent pas.

Revenons donc à la question. Une orbitale est une fonction mathématique qui décrit le chemin 3D d'un électron autour du noyau. Plutôt qu'une "orbite" planétaire, l'orbitale est une fonction de probabilité. La densité de l'orbite varie en fonction du rayon. En fonction de l'orbite, la fonction de probabilité montre également une orientation dans l'espace 3D. Ainsi, une orbitale S est sphérique en ce sens qu'il n'y a pas de préférence X-Y-Z. les orbitales P ont non seulement un aspect radial mais elles ont des orientations spatiales. Ainsi, les trois orbitales P sont comme des rotations 3D d'une rose à deux feuilles dans l'espace 2D. Les orbitales P ont donc des lobes orientés le long de l'axe +/- x, l'axe +/- y et l'axe +/- z.

Un mot d'avertissement. Les représentations orbitales sont très utiles pour prédire le comportement chimique, mais elles ne sont pas «réelles». Cela devient évidemment un peu fou lorsque quatre orbitales moléculaires $ sp ^ 3 $ sont formées chacune avec 25% de caractère S et 75% de caractère P! C'est un peu comme penser qu'une licorne est un hybride d'un cheval et d'un rhinocéros.

Je ne connais pas assez la physique pour savoir si c'est sur la cible ou non, mais ...

L'idée de différents modes vibrationnels est facile à démontrer avec un grand bol d'eau et votre doigt. Remplissez le bol et utilisez votre doigt pour exciter différents modèles d'ondes stationnaires sur la surface.

Commencez par le centre du bol, déplacez votre doigt lentement de haut en bas, et vous devriez être en mesure d'obtenir un onde stationnaire radialement symétrique qui ressemble à une version bidimensionnelle d'une orbitale 1S. Une fois que vous avez trouvé la fréquence fondamentale, doublez-la et vous obtiendrez quelque chose comme une orbitale 2S. Déplacez-vous hors du centre, et vous pourrez probablement exciter un mode qui ressemble à un 1P et un 2P.

Malheureusement, vous devrez vous arrêter là, car les modes d'ordre supérieur sur les deux dimensions la surface de l'eau n'a pas beaucoup de similitude avec les orbitales tridimensionnelles d'ordre supérieur.

Mais ce que vous pouvez montrer, c'est que les ondes stationnaires dans l'espace confiné du bol sont limités à seulement quelques types discrets possibles, et que pour chaque type, la fréquence semble toujours être un multiple entier d'une fréquence fondamentale.

Orbital est une fonction d'onde à un électron. Il décrit où un électron (ou une paire, si nécessaire) doit être attendu, ignorant en quelque sorte tous les autres électrons.

Un électron est à la fois une particule et une onde.

Les ondes sonores voyageant dans l'air libre peuvent avoir n'importe quelle fréquence. Mais un disque vibrant ne peut résonner qu'à certaines fréquences. Celles-ci correspondent aux modes de vibration du disque. Les animations en bas de https://en.wikipedia.org/wiki/Vibrations_of_a_circular_membrane montrent ces modes de vibration, et il existe une correspondance biunivoque avec les orbitales de symétrie s, p et d (des symétries orbitales plus complexes nécessitent 3 dimensions.)

Bien que cette analogie soit loin d'être parfaite, elle montre les principes d'une fonction d'onde. A noter que dans tous les cas sauf 1s, il y a une partie de la membrane qui ne bouge pas du tout. C'est ce qu'on appelle un nœud. Les nœuds peuvent être plans ou circulaires / sphériques. Dans une orbitale, un nœud est un endroit où la probabilité de trouver un électron est nulle.

Le nombre total de zones où la probabilité de trouver un électron est nulle (cela inclut la zone de distance infinie du atome) est donné par le nombre dans la désignation orbitale. Le nombre de nœuds plans est donné par la lettre.

Ainsi, toutes les orbitales de désignation 3 ont 3 zones où la probabilité de trouver un électron est nulle. 3s a 2 nœuds sphériques (la 3ème zone est à une distance infinie de l'atome.) 3p a un nœud plan et 1 nœud sphérique. 3d a 2 nœuds plans (ce qui lui donne la forme familière à 4 lobes.) Notez également qu'il existe une orbitale 3d avec un nœud conique, mais nous la considérerons comme appartenant au même groupe que les notes planaires.

En revenant à l'analogie du disque circulaire, nous voyons qu'il peut vibrer dans un certain nombre de modes discrets, et son mouvement peut être décrit comme une combinaison de ces modes.

Dans un atome, le principe d'exclusion de pauli dicte que tous les électrons doivent avoir des nombres quantiques différents. Ainsi, chaque orbitale peut contenir jusqu'à 2 électrons, à condition qu'ils aient des spins différents. De cette façon, l'atome diffère de l'analogie du disque vibrant, en ce que le disque peut vibrer avec n'importe quelle amplitude, mais une orbitale ne peut contenir que 0,1 ou 2 électrons.

Chaque électron a une certaine énergie, en fonction sur quelle orbitale il se trouve. L'énergie de l'électron dépend également de son interaction avec d'autres électrons dans d'autres orbitales. En grande partie à cause de ces interactions, nous constatons que les orbitales avec plus de nœuds plans sont à une énergie plus élevée que celles avec moins de nœuds plans.

Imaginez que j'étais votre petit frère, comment lui expliqueriez-vous une orbitale? (en supposant qu'il sache ce que sont les atomes, les électrons et les neutrons, et le reste des bases jusqu'à ce point).

Il y a un petit problème là-dedans, en ce sens qu'il ne saura probablement pas quoi les électrons sont. Il n'y a pas de modèle d'électrons dans le modèle standard. Elle est décrite comme une particule fondamentale, mais il n'y a aucune description réelle de la façon dont elle est créée dans la production de paires gamma-gamma ou de ce qu'elle est vraiment. Vous pouvez trouver des informations sur les spineurs et la ceinture de Dirac et l ' équation de Dirac, qui est une équation d'onde. Mais alors les gens parlent de particules ponctuelles et de probabilité et tout devient confus.

J'ai lu à ce sujet et je ne peux pas en faire la tête haute.

À mon humble avis, c'est facile lorsque vous faites un peu de travail de détective . Jetez un œil à l'article de Wikipédia sur les orbitales atomiques et notez que les électrons "existent sous forme d'ondes stationnaires" . Le point discutable est que lorsque vous sortez un électron d'une orbitale atomique, il existe toujours sous forme d'onde stationnaire. Vous l'avez fait avec un positron à partir de photons dans la production de paires gamma-gamma. Vous pouvez diffracter des électrons. Diffraction électronique "fait référence à la nature ondulatoire des électrons" . L'électron est une onde. Une vague debout . Onde stationnaire, champ debout. L'électron ne tourne pas autour du noyau comme une planète, c'est plutôt comme l'anneau électromagnétique de Saturne. Ce n'est pas plat, c'est sphérique, mais c'est difficile à imaginer, alors pour le décrire à votre petit frère, tenez-vous-en à un anneau plat. Pour le lui montrer, donnez-lui un cierge magique et faites-le tourner en rond. Cela donne une image en forme d'anneau, qui se rapporte à l'orbitale s ci-dessous:

_{Image fournie par UCDavis Chemwiki}

Maintenant, demandez-lui de faire pivoter le cierge magique en huit. Cela concerne l'orbitale p dans l'orientation x y ou z. Puis demandez-lui de faire tourner le cierge magique en forme de trèfle à quatre feuilles. Cela concerne une orbitale d, et ainsi de suite.

Comment les différents niveaux d'énergie se rapportent-ils à eux?

Parce que nous avons affaire à des ondes électromagnétiques plutôt qu'à des étincelles, et aux niveaux d'énergie sont un peu comme des engrenages. Voir cette image de Kenneth Snelson:

Il y a toujours un nombre entier de longueurs d'onde dans l'onde stationnaire. L'atome est un "oscillateur harmonique quantique". L'onde électronique peut effectivement changer de vitesse lorsqu'elle absorbe une onde photonique E = hf. Lorsqu'il émet un photon, il change effectivement de vitesse.

Bien sûr, les orbitales électroniques ne sont pas aussi simples que cela, mais cela devrait éloigner votre petit frère de la première base.

Je n'essaierais pas plus d'expliquer ce qu'est "une orbitale" "à mon hypothétique petit frère, que je ne le ferais à un chien. S'il y avait une raison de les expliquer, alors je devrais savoir ce que c'était. J'ai remarqué que vous n'avez même pas mentionné si vous parliez d'orbitales atomiques ou d'orbitales moléculaires ... Si elles sont poussées, je dirais que les orbitales décrivent la forme du volume de l'espace dans lequel l'électron lié avec un ensemble donné de nombres quantiques est probablement la forme de l'espace où cet électron passe le plus clair de son temps.

Les oribitals sont les emplacements où les électrons se déposent dans un atome stable. Ceci est basé sur deux hémisphères de la force faible "nucléomagnétique" de type magnétique sous-jacente du noyau à chaque électron maintenant les électrons dans une coquille. Cette force est répulsive là où la charge électrostatique est attractive. Je vois pourquoi les électrons restent dans le champ.

En conséquence, vous obtenez les premiers points d'équilibrage de la coquille aux deux extrémités des axes. Par conséquent, Hyrogen avec un et Helium avec deux, puis la sous-couche et la coquille sont pleines.

Après cela, les électrons remplissent deux hémisphères de plus en plus par carrés, donc la prochaine coquille est deux sous-coquilles. Ceci d'une pyramide qui construit 1/3/5/5/3/1 de pôle en équateur en pôle. Notez que 1 + 3 + 5 = 9 qui depuis un carré parfait. Pourtant, ceux-ci sont en deux hémisphères donc des sous-coquilles de taille 2, 6, 10. Et les coques complètes sont 2x1, 2x4, 2x9.

Voir mon livre sur le modèle atomique Scrunched Cube pour expliquer les coques et sous-coques pour les gens ordinaires.